Geometry and dynamics of lipid membranes: The Scriven-Love number

Abstract

The equations governing lipid membrane dynamics in planar, spherical, and cylindrical geometries are presented here. Unperturbed and first-order perturbed equations are determined and nondimensionalized. In membrane systems with a nonzero base flow, perturbed in-plane and out-of-plane quantities are found to vary over different length scales. A new dimensionless number, named the Scriven-Love number, and the well-known Föppl–von Kármán number result from a scaling analysis. The Scriven-Love number compares out-of-plane forces arising from the in-plane, intramembrane viscous stresses to the familiar elastic bending forces, while the Föppl–von Kármán number compares tension to bending forces. Both numbers are calculated in past experimental works, and span a wide range of values in various biological processes across different geometries. In situations with large Scriven-Love and Föppl–von Kármán numbers, the dynamical response of a perturbed membrane is dominated by out-of-plane viscous and surface tension forces—with bending forces playing a negligible role. Calculations of non-negligible Scriven-Love numbers in various biological processes and in vitro experiments show in-plane intramembrane viscous flows cannot generally be ignored when analyzing lipid membrane behavior.

Download paper here

Recommended citation: Amaresh Sahu, Alec Glisman, Joël Tchoufag and Kranthi K. Mandadapu. (2020). “Geometry and dynamics of lipid membranes: The Scriven-Love number.” Phys. Rev. E. 101(05240).

Figure 1

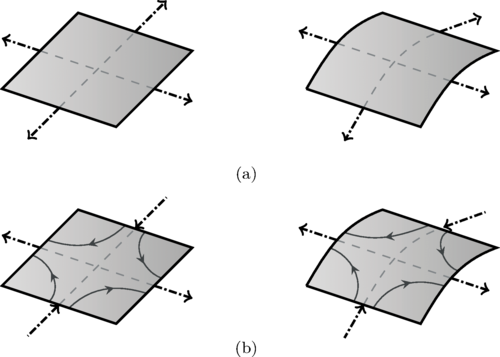
A schematic showing how surface tension (a) and viscous (b) forces arise in the normal direction, with dashed arrows depicting boundary tractions. (a) The surface tension pulls the membrane at each edge, such that when the shape is perturbed a normal force arises. (b) In an extensional flow, the velocity field is depicted by the solid arrows. The tractions push and pull the fluid, as shown with the dashed arrows, such that when the membrane is perturbed a viscous force arises in the normal direction.